Pengertian, Rumus dan Bunyi
Hukum Newton 1, 2, 3 serta Contoh Soal Hukum Newton
Pada
pembahasan sebelumnya kita telah mempelajari gaya. Gaya yang dikenakan atau diberikan
pada suatu benda dapat mengakibatkan perubahan bentuk dan atau gerak benda
tersebut. Kali ini kita akan mempelajari gerak benda dan gaya yang memengaruhi
gerak benda tersebut.
Permasalahan
gerak dan penyebabnya telah menarik perhatian para ahli filsafat alam selama
berabad-abad. Permasalahan ini mulai menemukan titik terang pada masa Galileo
dan Newton.
Pada abad
ke-17, Galileo menyadari bahwa suatu benda menjadi lebih lambat atau
lebih cepat jika sejumlah gaya bekerja pada benda tersebut. Jika gaya yang
bekerja pada benda dihilangkan maka benda akan terus bergerak pada garis lurus.
Galileo menyatakan bahwa suatu benda akan
mengalami perubahan kelajuan hanya saat benda dikenai suatu gaya. Dia juga
berpendapat bahwa suatu benda akan bertambah cepat atau melambat selama gaya
yang bekerja pada benda tidak saling meniadakan.
Berdasarkan
gagasan Galileo tersebut, seorang ilmuwan Inggris, yaitu Sir Isaac
Newton menjelaskan tentang gaya dan gerak.
Gagasan-gagasan
Newton dituangkan melalui ketiga hukumnya dalam buku berjudul Philosophiae
Naturalis Principia Mathemathica atau yang lebih dikenal sebagai Principia.
Ketiga hukum
tentang gerak dan gaya yang dikemukakan oleh Newton dikenal sebagai hukum
Newton. Hukum I dan II Newton mengikuti gagasan yang dikemukakan oleh Galileo.
Sedangkan
hukum III Newton membicarakan mengenai gaya aksi dan reaksi. Apa dan bagaimana
penerapan ketiga hukum Newton tersebut akan kita pelajari berikut ini.
Hukum I Newton
Bola
menggelinding karena diberi gaya dorong. Namun, bola tetap menggelinding
meskipun tangan tidak lagi menyentuh bola.
Dengan
demikian, bola tetap menggelinding meskipun tidak ada gaya yang bekerja pada
bola. Hal ini merupakan contoh dari hukum I Newton dalam kehidupan
sehari-hari.
Jika kita
berada di dalam sebuah bus yang sedang berhenti kemudian digas mendadak maka
badan kita akan terdorong ke belakang.
Hal ini
terjadi karena badan kita akan mempertahankan keadaan awalnya, yaitu diam. Bus
yang digas mendadak akan bergerak ke depan sehingga badan kita terdorong ke
belakang (berlawanan dengan arah gerak bus).
Berdasarkan
peristiwa di atas, dapat disimpulkan bahwa ketika gaya luar dihilangkan, setiap
benda akan berusaha mempertahankan keadaan awalnya, yaitu diam atau bergerak
lurus beraturan.
Rumus dan Bunyi Hukum 1 Newton
Hal ini
sesuai dengan hukum I Newton yang berbunyi:
Jika
resultan gaya yang bekerja pada benda sama dengan nol maka benda yang mula-mula
diam akan tetap diam dan benda yang mula-mula bergerak lurus beraturan akan
tetap bergerak lurus beraturan.
Secara
matematis, hukum I Newton dapat dituliskan sebagai berikut.
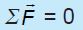
Keterangan:
F: resultan
gaya (N)
Sifat benda
yang mempertahankan keadaan awalnya disebut kelembaman atau inersia. Sehingga
hukum I Newton disebut juga hukum kelembaman. Kelembaman yang
dimiliki suatu benda diam membuatnya sulit digerakkan.
Akan tetapi
jika benda tersebut bergerak maka kelembamannya akan menyebabkan benda terus
bergerak lurus. Untuk melawan kelembaman benda diperlukan suatu gaya tertentu.
Gaya yang
diperlukan untuk melawan kelembaman sebanding dengan massa benda, karena
semakin besar massa benda tersebut, kelembamannya juga semakin besar.
Hukum II Newton
Kita telah
mempelajari tentang resultan
gaya pada pembahasan
sebelumnya. Masih
ingatkah kamu apa yang dimaksud dengan resultan gaya?
Sebagai
contoh; 2 orang anak sedang mendorong lemari. Resultan gaya yang bekerja pada
lemari merupakan penjumlahan dari gaya yang diberikan oleh masing-masing orang.
Resultan
gaya yang dialami lemari lebih besar daripada gaya yang diberikan oleh
masing-masing orang, sehingga lemari lebih mudah digeser.
Jika lemari
tersebut hanya didorong oleh salah satu orang dengan gaya yang lebih kecil
daripada resultan gaya kedua orang tersebut maka lemari akan lebih sulit
digeser. Dengan demikian, semakin besar gaya yang bekerja pada benda, benda
akan bergerak semakin cepat.
Jika kamu
mendorong sebuah meja dengan gaya yang besarnya sama dengan besar gaya yang
digunakan untuk menggeser lemari maka meja tersebut akan bergeser lebih cepat.
Jadi, dapat kita simpulkan bahwa semakin kecil massa suatu benda, benda akan
lebih cepat bergerak.
Rumus dan Bunyi Hukum 2 Newton
Peristiwa-peristiwa
di atas sesuai dengan hukum II Newton yang berbunyi:
Percepatan
yang ditimbulkan oleh gaya yang bekerja pada benda berbanding lurus dengan
besar gayanya dan berbanding terbalik dengan massa benda.
Secara
matematis, hukum II Newton dapat dirumuskan sebagai berikut.

Keterangan:
a :
percepatan benda (m/s2)
m : massa
benda (kg)
Contoh Penerapan Hukum 2 Newton
dalam kehidupan sehari-hari
Contoh
penerapan hukum II Newton dalam kehidupan sehari-hari adalah pada gerakan di dalam lift.
Ketika kita berada di dalam lift yang sedang bergerak, gaya berat kita akan
berubah sesuai pergerakan lift.
Saat lift
bergerak ke atas, kita akan merasakan gaya berat yang lebih besar dibandingkan
saat lift dalam keadaan diam. Hal yang sebaliknya terjadi ketika lift yang kita
tumpangi bergerak ke bawah.
Saat lift
bergerak ke bawah, kita akan merasakan gaya berat yang lebih kecil daripada
saat lift dalam keadaan diam. Cara penghitungan matematis dari hukum II Newton
dapat kamu simak pada contoh soal berikut ini.
Contoh Soal Hukum 2 Newton
Sebuah benda
bermassa 10 kg bergerak dengan percepatan 2 m/s. Berapakah besar gaya yang
diberikan pada benda?
Penyelesaian:
Diketahui:
m = 10 kg
a = 2 m/s
Ditanyakan:
F = . . .?
Jawab:
F = m . a
F = 10 . 2
F = 20 N
Jadi, gaya
yang bekerja pada benda adalah 20 N.
Hukum II
Newton juga dapat diterapkan pada gerak lurus, terutama gerak lurus berubah
beraturan (GLBB). Dalam GLBB berlaku persamaan berikut.

Untuk lebih
memahami penerapan hukum II Newton pada GLBB, simaklah contoh soal berikut!
Contoh soal Hukum 2 Newton pada GLBB
Sebuah mobil
bermassa 2.000 kg bergerak dengan kelajuan 16 m/s. Jika mobil tersebut direm
dengan gaya 8.000 N, berapakah jarak yang ditempuh mobil mulai direm sampai
berhenti?
Penyelesaian:
Diketahui:
m = 2.000 kg
v 0 = 16 m/s
v t = 0 m/s
(karena berhenti)
F = -8.000 N
Ditanyakan: s = . . .?
Jawab:
Langkah 1
Menentukan
perlambatan mobil, karena mobil mengalami pengereman maka percepatan bernilai
negatif.
F = m . a
-8.000
= 2.000 . a
a = -4 m/s
Langkah 2
Menentukan
jarak yang ditempuh selama perlambatan.
v2 =
v02 + 2 . a . s
0 =
162 +2 . (-4) . s
0 =
256 – 8s
8s = 256
s =
32 m
Jadi, jarak
yang ditempuh mobil dari mulai direm hingga berhenti adalah 32 m.
Hukum III Newton
Mengapa
ketika jari tangan kita menekan meja semakin kuat akan terasa sakit? Sebenarnya
ketika kita menekan meja berarti kita memberikan gaya pada meja.
Tangan kita
akan merasa sakit sebab meja akan memberikan gaya yang besarnya sama dengan
gaya tekan tangan kita, tetapi arahnya berlawanan.
Jadi, jika
kita perhatikan, gaya bukanlah sesuatu dalam benda tersebut tetapi merupakan
interaksi antara dua benda.
Rumus dan Bunyi Hukum 3 Newton
Peristiwa di
atas merupakan contoh dari hukum III Newton, yang dikenal sebagai hukum
aksi-reaksi, yang bunyinya:
Jika benda
pertama memberikan gaya pada benda kedua maka benda kedua akan memberikan gaya
yang besarnya sama tetapi arahnya berlawanan.
Secara
matematis, hukum III Newton dapat dinyatakan dengan rumus berikut.

Hukum III
Newton berlaku pada dua gaya yang merupakan pasangan aksi-reaksi. Dua gaya
dikatakan pasangan aksi-reaksi jika:
1. bekerja
pada dua benda yang berbeda,
2. saling
berinteraksi,
3. besarnya
sama dan berlawanan arah.
Untuk lebih
memahami hukum III Newton tentang gaya aksi-reaksi perhatikan gambar di bawah
ini!
 |
Gambar: Bola digantung dengan tali pada dinding
|
Pada gambar
di atas gaya-gaya yang bekerja adalah sebagai berikut.
F1 = gaya
yang diberikan tali pada dinding
F2 = gaya
yang diberikan dinding pada tali
F3 = gaya
yang diberikan bola pada tali
F4 = gaya
yang diberikan tali pada bola
w = gaya
berat bola
F1 dan F2
serta F3 dan F4 adalah pasangan gaya aksi-reaksi. Kedua pasang gaya tersebut
bekerja pada dua benda yang berbeda dan saling berinteraksi. Besar gaya F1 dan
F2 adalah sama tetapi arahnya berlawanan. Demikian pula dengan gaya F3 dan F4.
Sedangkan
gaya F2 dan F3 bukan pasangan gaya aksi-reaksi karena kedua gaya tersebut
bekerja pada satu benda yang sama, yaitu tali.
F3 dan w
bukan merupakan pasangan aksi-reaksi meskipun kedua gaya tersebut besarnya
sama, berlawanan arah, dan bekerja pada dua benda yang berbeda, karena kedua gaya
tersebut tidak saling berinteraksi.
Jadi, dari
kelima gaya tersebut yang merupakan pasangan aksi-reaksi adalah:
1. F1 dan F2
2. F3 dan F4
Contoh Penerapan Hukum 3 Newton
dalam kehidupan sehari-hari
Contoh
penerapan hukum III Newton dalam kehidupan sehari-hari dapat kita jumpai pada peristiwa
merapatnya perahu ke dermaga. Ketika tali perahu telah terikat ke dermaga namun
perahu belum merapat ke dermaga maka nelayan akan menarik tali perahu.
Nelayan tersebut
memberikan gaya tarik yang arahnya menjauhi dermaga, hal ini menyebabkan perahu
mendekat ke dermaga. Perahu dapat mendekat ke dermaga karena adanya gaya reaksi
yang arahnya berlawanan dengan gaya tarik yang diberikan oleh nelayan.